[KB2D]

Program [KB2D] służy do estymacji metodami prostego i zwykłego krigingu (SK i OK) dla danych dwuwymiarowych (oczywiście także jednowymiarowych). Jest to prosty algorytm, pozbawiony szeregu zaawansowanych opcji definiowania sąsiedztwa szukania (search neigborhood), oraz testowania jakości estymacji (kroswalidacja, walidacja podzbioru).

Wzorcowy (blank) plik parametrów

Plik parametrów z objaśnieniami po polsku

Uwaga: W efekcie działania [KB2D] uzyskuje się dwa pliki z wynikami obliczeń:

Ø Pierwszy z nich to plik tekstowy (ASCII) zawierający rejestrację etapowych wyników obliczeń. W pliku parametrów podaje się tak zwany „debugging level” w zakresie od 0 do 3. Im wyższa jego wartość, tym więcej wyników jest rejestrowane. Jeśli siatka interpolacyjna jest duża (dziesiątki tysięcy węzłów i więcej) oraz wybrano poziom 2 lub 3, to rozmiar wynikowego pliku może być bardzo duży (dziesiątki MB i więcej). Wysoki poziom rejestracji wybiera się wówczas, kiedy trzeba przeprowadzić analizę macierzy estymacji krigingowych dla poszczególnych węzłów siatki interpolacyjnej w celu identyfikacji przyczyn nieoczekiwanych rezultatów.

Ø Drugi to plik tekstowy (ASCII) w uproszczonym formacie Geo-EAS z dwoma kolumnami danych: wartości estymowanych i wariancji krigingowych dla kolejnych węzłów siatki interpolacyjnej. Są one pozbawione współrzędnych i uporządkowane najpierw według rosnących wartości współrzędnej Y, a później według rosnącego X. Tak uporządkowane dane można za pomocą programu [PIXELPLT] przedstawiać w postaci map rastrowych

Fragment zawartości pliku rejestracji etapowych wyników obliczeń metodą prostego krigingu (SK) przy „debugging level” równym 2.

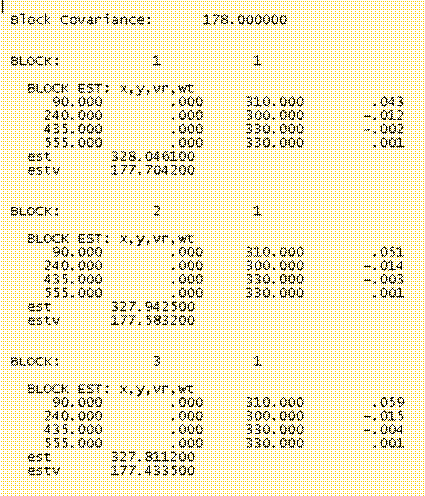
Ø Algorytm zawarty w programie [KB2D] umożliwia wykonanie zarówno estymacji punktowych (point kriging), jak i blokowych (block kriging). Block kriging to nazwa własna procedur umożliwiających szacowanie średniej wartości dla fragmentu profilu, wycinka powierzchni czy objętości o dowolnym rozmiarze i kształcie. Potrzeby uzyskania takich wartości są zazwyczaj praktyczne. Dla rolnika nie jest ważne jakie są właściwości gleby w określonym punkcie pola. Ze względu na rodzaj urządzeń którymi się posługuje do nawożenia, nawadniania, czy też siania interesuje go średnia wartość cechy gleby na powierzchni równej zwykle kwadratowi szerokości tzw. „pasa uprawy”, czyli w warunkach polskich ok. 5² m². Podobnie górnika nie interesuje zawartość rudy w konkretnym kawałku skały, tylko średnia jej koncentracja dla „jednostki” objętości skały, która jest później przetwarzana w zakładzie przeróbki rudy, czyli na przykład jednej „łyżki” koparki, czy kombajnu górniczego, która może wynosić 1 m³ lub więcej. Pomiary, na podstawie których dokonujemy takiego szacowania, mają zazwyczaj charakter w przybliżeniu punktowy np.: próbka gleby, czy segment rdzenia wiertniczego. Dlatego też musimy się borykać z problemem oceny cechy w innej skali przestrzennej niż dane pomiarowe, co w geostatystyce określane jest jako „data support problem”. Wbrew temu co można by przypuszczać kriging blokowy nie polega na uśrednieniu n wartości określonych za pomocą punktowego krigingu wewnątrz określonej powierzchni, czy też objętości. W rzeczywistości w układzie równań zwykłego krigingu (OK) prawa ich część, czyli kowariancje danych do nieznanej wartości (point-to-unknown covariance) zastąpiona zostaje przez kowariancje danych do bloku (point-to-block covariance). W praktyce kowariancje danych do bloku są aproksymowane za pomocą średniej arytmetycznej kowariancji między punktem danych i N punktami wyznaczonymi wewnątrz bloku. W pliku parametrów [KB2D] musimy podać ile ma być takich punktów wzdłuż osi X i Y. Podanie „1” i „1” skutkuje wykonaniem obliczeń punktowego krigingu (point kriging), podanie „3” i „4” – obliczeniami blokowego krigingu, w których blok jest kwantyfikowany za pomocą 12 punktów (3 ´ 4 = 12). Ważnym problemem jest takie określenie ilości punktów kwantyfikujących blok aby nie wypływało to na zbytnie wydłużenie obliczeń, ale jednocześnie dawało jak najbardziej dokładne przybliżenie kowariancji danych do bloku i kowariancji bloku do bloku. Zazwyczaj zaleca się, aby tych punktów było co najmniej (4)ⁿ, gdzie n oznacza ilość wymiarów bloku (czyli 4 dla profilu, 16 dla powierzchni i 64 dla objętości). Kiedy jakość uzyskanych wyników jest kluczowa, powinno wykonywać się powtarzalne obliczenia dla stopniowo powiększanej liczby punktów kwantyfikujących blok. Optymalny wybór następuje w momencie kiedy wyniki kolejnych obliczeń różnią się już bardzo nieznacznie. Należy pamiętać, że w przypadku estymacji punktowej otrzymujemy wartości charakteryzujące lokalizacje węzłów siatki interpolacyjnej, natomiast blokowej – średnie wartości dla oczka siatki.